Here we consider problem 6 of the recent Romanian Master of Mathematics competition – a very difficult problem. Nobody solved it during the tournament. Let me point out a very similar problem – RMM Shortlist 2020, A1 – see [3], proposed by the same author. I think it’s of similar difficulty. In my opinion both are not suitable for a high school Olympiad level, although I like them because it’s real math. Maybe they fit for Miklos Schweitzer competition, but on the other hand both problems are known results – the current one by Filaseta and Konyagin – see [2] – so the papers can easily be found by searching the web.
Problem (RMM 2024, problem 6). A polynomial 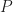 with integer coefficients is square-free if it is not expressible in the form
with integer coefficients is square-free if it is not expressible in the form  , where
, where 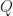 and
and 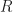 are polynomials with integer coefficients and
are polynomials with integer coefficients and 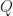 is not constant. For a positive integer
is not constant. For a positive integer 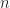 , let
, let 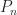 be the set of polynomials of the form
be the set of polynomials of the form

Prove that there exists an integer 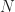 such that for all integers
such that for all integers  , more than
, more than  of the polynomials in
of the polynomials in 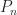 are square-free.
are square-free.
(Navid Safaei, Iran)
The proof is based on the ideas I saw in [4] and consists of 3 main statements. The proof of the last one is a version of a problem we did in a blogpost here – see [1].
It boils down to prove that if we take a random polynomial in  the probability that it is not square-free tends to
the probability that it is not square-free tends to  as
as  Hereafter, we refer to polynomials in
Hereafter, we refer to polynomials in 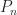 that are not square-free as bad polynomials, and to the square-free ones as good. So, in other words, if we take a random polynomial in
that are not square-free as bad polynomials, and to the square-free ones as good. So, in other words, if we take a random polynomial in  the probability that it is bad tends to
the probability that it is bad tends to  as
as  Here are the milestones of our plan.
Here are the milestones of our plan.
- Claim 1. We’ll show that if we fix a natural number
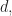 the probability of taking a bad polynomial
the probability of taking a bad polynomial 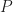 in
in 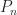 with
with  and
and  can be made as small as we want if
can be made as small as we want if 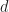 is large enough.
is large enough.
- Claim 2. We prove that there are finitely many
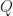 with integer coefficients and
with integer coefficients and  for which there exists
for which there exists 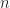 and
and  such that
such that 
- Claim 3. We prove that for each fixed polynomial with integer coefficients
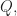 the probability of taking a polynomial
the probability of taking a polynomial  so that
so that 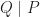 tends to
tends to  as
as 
Suppose that we already have the above three claims proven. The second claim ensures that there are only finitely many integer polynomials  with degrees less than
with degrees less than 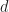 that can divide a binary polynomial
that can divide a binary polynomial 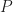 .
.
For any fixed 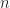 we take a random polynomial
we take a random polynomial  and let us introduce the following events. Hereafter,
and let us introduce the following events. Hereafter, 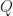 denotes a polynomial with integer coefficients.
denotes a polynomial with integer coefficients.




Apparently,

which implies

Fix some  The first claim shows that we can choose sufficiently large
The first claim shows that we can choose sufficiently large 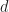 such that for any
such that for any  we have
we have  According to the third claim, we can choose
According to the third claim, we can choose 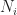 such that for
such that for  we have
we have 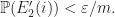 Therefore, for
Therefore, for  we have
we have

This means that the probability of taking a bad polynomial can be made as small as we want by choosing a sufficiently large 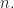 It remains to prove the three statements.
It remains to prove the three statements.
Proof of Claim 1. Dealing with large squares dividing binary polynomials.
Let 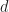 be a natural number. Hereafter,
be a natural number. Hereafter, 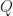 and
and 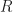 denote polynomial with integer coefficients and
denote polynomial with integer coefficients and 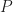 is a binary polynomial of degree
is a binary polynomial of degree 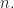 Suppose
Suppose  where
where 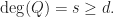 We reduce the polynomials
We reduce the polynomials  modulo 2, i.e. we substitute each coefficient with its residue modulo 2, thus obtaining new polynomials
modulo 2, i.e. we substitute each coefficient with its residue modulo 2, thus obtaining new polynomials  (
(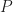 remains the same). Clearly
remains the same). Clearly

We can assume that 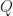 is a monic polynomial, hence
is a monic polynomial, hence  Clearly,
Clearly,  Since
Since  has
has 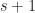 binary coefficients and
binary coefficients and  has
has  ones, all possible options for them are
ones, all possible options for them are  Thus, the number of polynomials
Thus, the number of polynomials 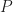 that satisfies
that satisfies 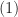 is at most
is at most  Therefore,
Therefore,

This yields,

which proves Claim 1.
Proof of Claim 2. Only finitely many “small” polynomials can divide a binary polynomial.
Let 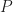 be a binary polynomial of degree
be a binary polynomial of degree 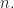 First to see that all roots of
First to see that all roots of 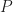 lie in the disk
lie in the disk  Assume on the contrary
Assume on the contrary  and
and  Then
Then


contradiction. Suppose now  and the senior coefficient of
and the senior coefficient of 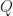 is
is  Let
Let  are the roots of
are the roots of 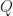 . The magnitude of all of them is less than
. The magnitude of all of them is less than 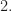 Using the Vieta formulas, we see that the coefficients of
Using the Vieta formulas, we see that the coefficients of 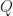 are less than some expression that depends only on
are less than some expression that depends only on  Since these coefficients are integers, the options for
Since these coefficients are integers, the options for 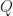 are finitely many, they are bounded by some constant that depends only on
are finitely many, they are bounded by some constant that depends only on 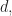 but not on
but not on 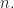
Proof of Claim 3. The probability that a binary polynomial is a multiple of a fixed polynomial is small.
Let 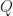 be a fixed polynomial of integer coefficients and suppose
be a fixed polynomial of integer coefficients and suppose  Let
Let 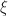 be a root of
be a root of  It follows
It follows  Note that
Note that  that’s why
that’s why 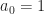 in the definition of
in the definition of  Take the set
Take the set  . Let us first consider the case when
. Let us first consider the case when  , i.e.
, i.e. 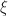 is not a root of unity. The equality
is not a root of unity. The equality
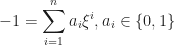
just means that the sum of elements of some subset of 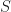 is
is 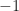
Lemma 1. Let 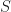 be a set of
be a set of 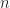 distinct complex numbers and
distinct complex numbers and  The probability that the sum of the elements of a random subset of
The probability that the sum of the elements of a random subset of 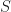 is
is  is less than
is less than 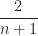 .
.
Proof. I considered and proved this claim in a blog post, see [1]. Call a subset of 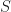 bad if the sum of its elements is
bad if the sum of its elements is 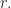 As usual, a subset of
As usual, a subset of 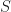 can be represented as a binary vector
can be represented as a binary vector  each bit indicates if an element is in the set or not. The idea is simple. For any binary vector
each bit indicates if an element is in the set or not. The idea is simple. For any binary vector 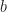 that corresponds to a bad subset we consider the unit sphere (by Hamming distance) centered at
that corresponds to a bad subset we consider the unit sphere (by Hamming distance) centered at 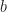 , that is, the set of all binary vectors that differ from
, that is, the set of all binary vectors that differ from 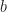 at exactly one bit. Their number is
at exactly one bit. Their number is 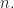 Non of them is a bad binary vector. That is, each bad binary vector is surrounded by
Non of them is a bad binary vector. That is, each bad binary vector is surrounded by  good ones. A bit care is needed to ensure that the unit spheres corresponding to distinct bad vectors do not intersect – see in [1]. So, the estimate follows.
good ones. A bit care is needed to ensure that the unit spheres corresponding to distinct bad vectors do not intersect – see in [1]. So, the estimate follows. 
Claim 3 follows from Lemma 1 if 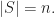 It remains to consider the case when
It remains to consider the case when  is a multiset. Note that
is a multiset. Note that  since
since  Let
Let  be he the smallest number with
be he the smallest number with 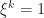 . We have a multiset
. We have a multiset 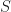 with
with  groups, each one consists of (almost)
groups, each one consists of (almost) 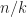 equal values. If
equal values. If  is large (e.g.
is large (e.g.  ), we can do the same trick as in Lemma 1 (flipping the bit of the first element of each group – we can number them) and obtain that the probability of taking a bad binary vector is less than
), we can do the same trick as in Lemma 1 (flipping the bit of the first element of each group – we can number them) and obtain that the probability of taking a bad binary vector is less than  .
.
In case  is small (
is small ( ), we take the group
), we take the group  with the largest number of elements, say
with the largest number of elements, say  . Take a bad binary vector
. Take a bad binary vector 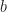 and let the number of chosen elements that are in
and let the number of chosen elements that are in  is
is  . Since all the elements in
. Since all the elements in  are the same (they have the same value), every binary vector with the same bits as
are the same (they have the same value), every binary vector with the same bits as 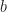 outside
outside  , and such that the number of 1’s bits corresponding to the elements of
, and such that the number of 1’s bits corresponding to the elements of  is different from
is different from  is not bad. So, the portion of the bad vectors for any fixed binary values corresponding to elements outside
is not bad. So, the portion of the bad vectors for any fixed binary values corresponding to elements outside  is at most
is at most
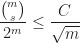 .
.
where  is a constant. Therefore, the probability of taking a bad binary vector is less than
is a constant. Therefore, the probability of taking a bad binary vector is less than ![\displaystyle \frac{C}{\sqrt m}\le \frac{C}{\sqrt[4]{n}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cfrac%7BC%7D%7B%5Csqrt+m%7D%5Cle+%5Cfrac%7BC%7D%7B%5Csqrt%5B4%5D%7Bn%7D%7D&bg=ffffff&fg=1a1a1a&s=0&c=20201002)
This means that for a fixed polynomial 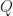 , the probability of randomly taken
, the probability of randomly taken  is multiple of
is multiple of 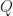 is
is  so it tends to zero as
so it tends to zero as 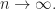
Comment
This solution has several crucial moments. The most difficult part (in my opinion) is to see that the probability of a binary polynomial 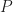 be multiple of
be multiple of  where
where 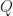 is an integer polynomial of some large degree, is small (it’s
is an integer polynomial of some large degree, is small (it’s  ). It involves a reduction modulo
). It involves a reduction modulo 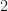 . The second part is to see that there are only finitely many polynomials with small degrees that can divide some binary polynomial
. The second part is to see that there are only finitely many polynomials with small degrees that can divide some binary polynomial  To see this we bound their coefficients. This is not hard to see, but it’s meaningful only if you got the first idea. In the third place comes the idea that for any fixed
To see this we bound their coefficients. This is not hard to see, but it’s meaningful only if you got the first idea. In the third place comes the idea that for any fixed 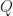 , the portion of the binary polynomials multiple of
, the portion of the binary polynomials multiple of 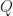 tends to
tends to  as
as  . I would say that it’s doable in real time, but only if you get to that point.
. I would say that it’s doable in real time, but only if you get to that point.
References.
[1] Hamming distance in Olympiad problems. Part 2.
[2] Squarefree values of polynomials all of whose coefficients are 0 and 1, M. Filaseta, S. Konyagin, Acta Arith., 74(3): 191-205, 1996
[3] A polynomial with coefficients +/-1 very likely to be irreducible. RMM 2020 Shortlist.
[4] AoPS thread on this problem
such that for each sequence
, there are infinitely many pairs
such that
. In fact, the official solution in the shortlist shows that
works. It uses a bit (just a bit) of calculus. We discussed this problem in the Bulgarian BMO 2024 camp and during the lecture Marin Hristov (BGR 1 and gold medal from BMO 2024) also solved it using an estimate of the partial sum of harmonic series. His solution is easier than mine. It yields
.
. By the way, I think that any constant
works (
doesn’t), but I don’t know how to prove it.
and
be any sequence as in the statement. Arguing by contradiction, suppose that there only finitely many pairs
that satisfy
Fix some
and view on the process of consecutively choosing the first
points
in
as being a tree with a root
which represents the interval
and each next point subsequently splits some interval into 2 subintervals – see fig.1 (the left graph is
and
is on the right side).
Its leaves (each one ends with an arrow) are the final intervals the interval
is split into, after
steps. Let us delete those edges
of
that are terminal edges, that is, no other directed edge starts from
Let the remaining tree is
There are three types of vertices in
The ones that have degrees
and
(we don’t count the root
). Denote the corresponding sets as
and
respectively. Let
We have
in order to get
are just the ones that represent the final intervals that
is partitioned into. Hence,
Each vertex
corresponds to some
for which
Denote this correspondence as
For each
there is only one directed terminal edge
that starts from
It corresponds to an interval
For
there are two terminal edges that originate from
Let us denote the corresponding intervals as
and let
Except for finitely many (exceptional) vertices
, it holds
with
because the worst-case scenario is when the set
\} consists of the first
smallest numbers. This is where an improvement can be made. If it is indeed the situation for the first
vertices, it would be not like that if we put, say, some additional
vertices.
and
does not depend on
because
is bounded as
Since
and
it further yields,
we obtain
using
which means
decreases in
so its minimum value is attained when
From
it follows
but it is not true when
is large enough, contradiction.








